Extraido de mi Diario, 1 de Octubre de 2006

No seré yo
No con mis palabras tu corazón podrá sentir,
tampoco mis caricias en tu piel conseguirán,
que tu pienses que soy yo el único guardián,
de la celda que mantiene oculto y sin salir,
el amor que todos ellos intentaron capturar,
pero ninguno hasta ahora ha logrado recibir.

Si lo fuera
Tu cuerpo, tu mente, tu alma cada día,
podría disfrutar del reflejo de un sueño,
no una ilusión, sino amor real, alegría,
si tu me nombraras para siempre el dueño,
de tus caricias, susurros y besos, vida mía.

Nota del Autor:
A mi me gusta más el primero por que la suma de los caracteres en cada línea es exactamente igual en todos los versos incluyendo espacios y símbolos de puntuación (sé que soy raro)
😀

Rafa.

Dada una situación ó estado actual X, que afronte 2 eventos aleatorios y excluyentes (de identicas probabilidades) que deriven a la consecución de un estado A ó de un estado B siendo ambos contrarios y complementarios, diremos que… Conociendo el posible resultado de A, podremos hallar el resultante de B y viceversa.

Representación del Teorema Simple

Deducimos desde el Factor Dilema que …

A= (2*X)-B

B=(2*X)-A

Para la aplicación del teorema es importante tener presente que ambos posibles eventos deben ser complementarios y excluyentes, y sobre todo que ambos disponen de idénticas probabilidades de darse (50% y 50%)

Ejemplo de aplicación (Trading/Bolsa):

Disponemos de unos ahorrillos y hemos pensado adquirir acciones de una empresa al parecer, con mucho futuro (pongamos que se llama Chicharrón, S.A.)
Queremos invertir 500 eur en acciones de esta empresa y nuestro corredor de bolsa sólo nos habla de lo mucho que podemos ganar.
Según dice, si la cotización sube 10 puntos, conseguiremos una rentabilidad del 15%, pero no nos dejó claro como nos quedaremos si ocurre lo contrario y la cotización baja 10 puntos.
La aplicación de la fórmula es muy simple…

B = (2X)-A … B = (2×500) – (500+15%) … B = 1000 – 575 … B = 425

Ejemplo (diversión):

Pedro es feo, bajito, calvo, cojo y gordo, aunque en realidad su mayor problema es su desdichada forma de vestir.
La ropa que usa le sienta fatal y Pedro sufre por ello. En el bar las mujeres lo miran y entre burlas, valoran su forma de vestir con un 4 sobre 10 (puntuación esta última atribuible al hombre más elegante y bién vestido que ninguna de ellas pudiera llegar a catar)
Pedro ya cansado de tanta burla, por fín se ha decidido a cambiar el vestuario. Nunca más le ofrecerán las cáscaras del melón cuando acuda a un restaurante.
Ya en la tienda de ropa, a Pedro le indican que (desgraciadamente) sólo disponen de un par de trajes que puedan ajustarse a su extremada talla y decadente semblante.
Al parecer ambos trajes fueron creados a partir de otro cuyo diseño pasó de moda, y con unas piezas confeccionaron el traje (A) y con otras confeccionaron el traje (B)
Nuestro amigo se prueba el primer traje (A) que la dependiente tiene más a mano. En el probador Pedro se sorprende grátamente al mirarse al espejo. Con lágrimas en los ojos ríe al verse más guapo que nunca, más guapo incluso que aquella vez posando ante los espejos deformes del circo. Tan contento está que lo compra sin siquiera preguntar por el otro traje. Pedro sale corriendo en dirección al bar de siempre, armado con su nuevo «look» demostrará a todos que incluso él puede cambiar si se lo propone.
Las encantadoras chicas que solían reirse de nuestro pintoresco sujeto, esta vez muestran seriedad en la mirada, valorando por sorpresa su nueva forma de vestir con un 7.
Entonces… que se ha perdido Pedro al dejar el otro traje (B) ?

B=(2*X)-A … B =(2*4)-7 … B = 1

Dados los resultados… mejor que Pedro ni pregunte por el otro traje…
Nótese que la fórmula ofrece la flexibilidad de devolver valores negativos… (Un resultado de -3, podría decirse que Pedro con ese traje acabaría detenido por escándalo público)

El Factor Dilema y sus Teoremas derivados son ideas originales de Rafael Jimenez Tocino.

Calcula un índice o puntuación basado en las distintas posibilidades que ofrece como resultado una acción propuesta para valorar la conveniencia o nó de ser afrontada.
En realidad, no es más la fórmula que la manera de usarla y aplicarla, además de la interpretación y uso de los resultados que ofrece.

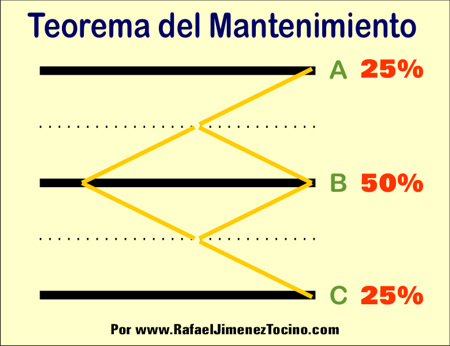
Este cálculo determinará (bajo condiciones de equidad 50%-50% en su fórmula simple ó definiendo las distintas probabilidades en su expresión compleja), si merece la pena comenzar ó mantener una actividad/acción/trabajo, modificarla, finalizarla/desistir de comenzarla, o símplemente optar por elegir otra diferente.

El Factor Dilema es la valoración global sobre las distintas posibilidades a las que una acción puede llegar a derivar, para poder compararla con otras valoraciones o con con la situación actual (antes de emprender tal acción). Nos permitirá determinar matemáticamente si merece la pena (o nó) efectuar dicha acción.

Dado un dilema, procederemos a calcular el factor sobre los distintos posibles resultados derivados de la acción a emprender usando sus respectivas probabilidades porcentuales.  Después compararemos dicho factor calculado con el Factor Dilema derivado de la situación actual o el de otro dilema.
Si el Factor hallado es superior al usado para compararlo, entonces nos interesará efectuar dicha acción, en caso contrario deberemos mantener la situación actual u optar por otra con mejor factor.

FD simple= (A+B)/2

Donde A y B son los 2 posibles resultados con probabilidad del 50% y 50%

FD complejo= (A*Pa + B*Pb + C*Pc)/100

Donde A,B,C… son los posibles resultados y Pa,Pb,Pc… sus respectivas probabilidades

De manera inversa, para hallar A y B…

A= (2*FD)-B    y    B=(2*FD)-A

y en la fórmula compleja para resolver los parámetros A, B y C …

A=((FD*100)-(B*Pb + C*Pc)) / Pa

B=((FD*100)-(A*Pa + C*Pc)) / Pb

C=((FD*100)-(A*Pa + B*Pb)) / Pc

En base a un resultado binomial y en condiciones de equidad de probabilidades (fórmula simple), deducimos que…

Ejemplo de uso del Factor Dilema (simple):

En un combate de boxeo los pújiles se llaman Pepe y Juan. Las apuestas están 3 a 1 a favor de Pepe.
Las cuotas(Odd) serían de 3(Pepe) contra 1(Juan), lo que indica que hay menos probabilidades de que gane Pepe pero si apostamos por el y consigue ganar, nos embolsaremos más dinero.
Con 1 euro en el bolsillo, y teniendo en cuenta que desde nuestra experta opinión ambos contrincantes tienen las mismas posibilidades de ganar, se nos presentan las siguientes posibilidades…
1. No apostar. Si nos vamos a casa, acabaremos con 1 euro, y si a casa nos vamos, acabaremos con 1 euro. Balances posibles: +1 contra +1 … FP=1 (BASE COMPARACIÓN)
2. Apostamos el euro por Juan. Si gana, acabaremos con 2 euros y si pierde nos quedaremos sin nada. Balances posibles: +2 contra 0 … FP=1 (NO INTERESA, NO SUPERA LA BASE)
3. Apostamos el euro por Pepe. Si gana acabaremos con 3 euros y si pierde nos quedaremos sin nada. Balances posibles: +3 contra 0 … FP=1,50 (SI INTERESA)
4. Apostamos 0,5 euros por Pepe y 0,5 euros por Juan (mitad y mitad). Balances posibles: +2 contra +1 … FP=1,50 (SI INTERESA)
5. Apostamos 0,75 eur por Pepe y 0,25 eur por Juan. (más al que más ofrece). Resultados posibles: 3 contra 0,5 … FP=1,75 (SI INTERESA)
(la situación del ejemplo es dificil que se nos presente, pues si las apuestas estan 3 a 1 a favor de Pepe es porque éste es un alfeñique y Juan posíblemente será un cacho bestia.)

Ejemplo de uso del Factor Dilema (compuesto):

Voy caminando por el bosque, tranquilo, con un estado anímico diríamos que: normal. Me encuentro en un cruce con 3 caminos ante mí y aparece un duende enano que me dice: «Caminante, estos son los 3 caminos mágicos: uno de ellos te hará más feliz y el otro te hará más triste en la misma proporción. Sin embargo el tercero no te influirá en nada.». Mirándole con ojos extrañados, por lo feo que era, me siento sobre una mohosa piedra que me moja el culo y calculo. El FD resulta ser 0. Me doy la vuelta y me vuelvo a casa.

El Factor Dilema y sus Teoremas derivados son ideas originales de Rafael Jimenez Tocino.

Extraido de mi diario, 1 julio 2008

El niño no callaba: “Lo quiero, lo quiero, lo quiero… “, lloraba y pataleaba exigiendo su premio.

Finalmente comprendió que jamás conseguiría colmar su eventual anhelo. Al final sólo aquél viejo balancín caballito de madera negro, golpeado, rallado, desconchada su pintura, esa que un día protegió su pulida y veteada piel de las largas jornadas cabalgando por el duro y espartano desierto, sólo aquel desgastado équido conseguiría acallar los deseos de su corazón, a todo trote huyendo de los temidos pieles rojas a lo largo de la profundidad del pasillo iluminado por el brillo de la cera sobre el terrazo.

Entendió que en esta vida hay que saber plantarse a la hora de elegir. Hay que saber cual es el verdadero deseo. Y ese deseo es, en todos los casos la felicidad.

Él comprendió que mientras lloraba en aquel rincón lamentándose de su miserable vida por no haber conseguido hacerse con aquel sofisticado videojuego, su hermanito pequeño se divertía con el viejo caballito, y que en verdad eso era lo que importaba, el tener, el vivir, el conseguir mantener esos instantes en los que la alegría nos ciega de la realidad de nuestras vidas, en los que puedes considerar que ese instante eres realmente feliz.

Buscamos y re-buscamos, deshechando la mayor parte de esos feos o imperfectos juguetes durante nuestro camino, pensando quizás que más allá habrá algo mejor.

Cuando con el tiempo llegamos a haber sufrido el eco de nuestras palabras en la intimidad de la alcoba, entonces nos percatamos de que en realidad no hay un final en el camino, únicamente hay un duro y solitario recorrido. Un viaje que no acaba de llevarnos a ninguna parte y que sólo nos deja los recuerdos de las estaciones en las que pudimos bajarnos, paradas poco interesantes entonces, que ojalá volvieran a presentarse.

Pero ya es tarde, y nuestra avaricia ha roto el saco de los deseos y nos quedamos con el agujero de la soledad. Y ya este tren no parará ni en las malas estaciones; entonces es cuando comprendemos que a la mayoría de las personas en nuestra situación lo que más nos aisla es nuestra própia lucha por conseguir la mejor compañía.

Rafa.

El otro día descubrí que hay ocasiones en las que las leyes de las probabilidades pueden «doblarse» o ser conceptuadas en un sentido distinto al que impone el universo de las matemáticas.

Voy a explicaros mi idea:

En una explanada limpia, sin ningún objeto en kilómetros a la redonda, hay marcadas en el suelo 3 líneas paralelas las cuales están separadas de manera equidistante varios metros entre sí.

Con los ojos tapados nos situamos sobre la línea central (y alguien nos desorientará dándonos whisky o girándonos sobre nuestro própio eje). Una vez mareados, un gracioso nos propondrá caminar a lo loco hasta que se acabe el camino o hasta que toquemos una de las 2 líneas exteriores:

. Llegar a tocar la línea de nuestra izquierda (A)
. Acabar en la misma línea (central) en la que estamos (B)
. Llegar a tocar la línea de nuestra derecha (C)

Según las leyes de la probabilidad, la posibilidad aleatoria excluyente de concluir en cada uno de los 3 puntos debería ser el 33,33%.
Si analizamos la situación en relación a la posición de partida, existe un 50% de probabilidades de acabar en la misma linea central (B) y un 25% de acabar en las líneas laterales.

Teorema del Mantenimiento

En un recorrido aleatorio, las posibilidad de acabar en el punto de partida es superior a la de terminar en puntos remotos equidistantes al mismo pues en cada momento la distancia entre la línea exterior y el centro… es la misma.

De esta forma, durante el recorrido hasta por fin tocar una de las líneas exteriores pisaremos muchas más veces la línea central desde donde hemos partido.

No se si servirá para algo, pero me ha parecido interesante compartirlo con vosotros.

Rafa.

Esta ciudad es atravesada por el río Pregolya, el cual se bifurca para rodear con sus brazos a la isla Kneiphof, dividiendo el terreno en cuatro regiones distintas, las que entonces estaban unidas mediante siete puentes llamados Puente del herrero, Puente conector, Puente verde, Puente del mercado, Puente de madera, Puente alto y Puente de la miel.

El problema fue formulado en el siglo XVIII y consistía en encontrar un recorrido para cruzar a pie toda la ciudad, pasando sólo una vez por cada uno de los puentes, y regresando al mismo punto de inicio.

Este es un célebre problema matemático, resuelto por Leonhard Euler en 1736 y cuya resolución dio origen a la teoría de grafos. Su nombre se debe a Königsberg, el antiguo nombre que recibía la ciudad rusa de Kaliningrado, que durante el siglo XVIII formaba parte de Prusia Oriental, como uno de los ducados del Reino de Prusia.

El problema consistía en responder a la siguiente pregunta:

Problema de los 7 puentes de Königsberg

Dado el mapa de Königsberg, con el río Pregolya dividiendo el plano en cuatro regiones distintas, que están unidas a través de los siete puentes, ¿es posible dar un paseo comenzando desde cualquiera de estas regiones, pasando por todos los puentes, recorriendo sólo una vez cada uno, y regresando al mismo punto de partida?

Pues bién, la solución propuesta por este señor fué decir que NO hay solución. 😛

Bueno, después de un par de horas pensando y analizando detalladamente los detalles de la pregunta, propongo mi solución…

Solución que propongo al problema de los 7 puentes de Königsberg

Si os fijáis, se cumplen todas las premisas: Empieza y acaba en el mismo punto, pasa por todos los puentes y los recorre sólo 1 vez (no dice nada de si se puede hacer mitad y mitad).
Espero que os hayáis divertido con esto 😉

Rafa.

Bueno, parece que el Blog ya está instalado en su mayor parte, espero que disfrutéis leyéndome.

Saludos a todos.

🙂