El otro día descubrí que hay ocasiones en las que las leyes de las probabilidades pueden «doblarse» o ser conceptuadas en un sentido distinto al que impone el universo de las matemáticas.
Voy a explicaros mi idea:
En una explanada limpia, sin ningún objeto en kilómetros a la redonda, hay marcadas en el suelo 3 líneas paralelas las cuales están separadas de manera equidistante varios metros entre sí.
Con los ojos tapados nos situamos sobre la línea central (y alguien nos desorientará dándonos whisky o girándonos sobre nuestro própio eje). Una vez mareados, un gracioso nos propondrá caminar a lo loco hasta que se acabe el camino o hasta que toquemos una de las 2 líneas exteriores:
. Llegar a tocar la línea de nuestra izquierda (A)
. Acabar en la misma línea (central) en la que estamos (B)
. Llegar a tocar la línea de nuestra derecha (C)
Según las leyes de la probabilidad, la posibilidad aleatoria excluyente de concluir en cada uno de los 3 puntos debería ser el 33,33%.
Si analizamos la situación en relación a la posición de partida, existe un 50% de probabilidades de acabar en la misma linea central (B) y un 25% de acabar en las líneas laterales.
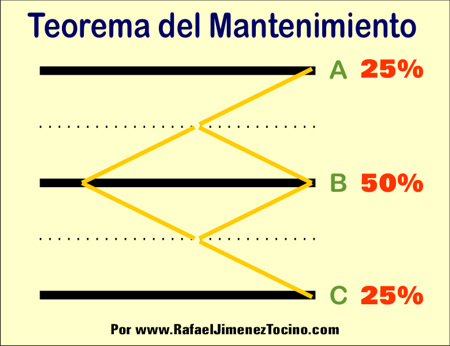
Teorema del Mantenimiento
En un recorrido aleatorio, las posibilidad de acabar en el punto de partida es superior a la de terminar en puntos remotos equidistantes al mismo pues en cada momento la distancia entre la línea exterior y el centro… es la misma.
De esta forma, durante el recorrido hasta por fin tocar una de las líneas exteriores pisaremos muchas más veces la línea central desde donde hemos partido.
No se si servirá para algo, pero me ha parecido interesante compartirlo con vosotros.
Rafa.